Deriving Guitar Theory in ~400 Lines of Python
Note: all the code for this article can be found here as a Github gist.
This article looks at applying basic music theory to the guitar using Python in order to derive chords and scales for alternate tunings.
This is a follow-up to my previous article on learning basic music theory in Python. Some of this stuff will make more sense if you’ve read the previous article, so I highly recommend doing so. (Given the various fretboard diagrams in this article, you might want to read on a desktop or in landscape mode if on a mobile.)
You might ask yourself: why do this? My primary reason is purely practical: I’ve been playing in an alternate tuning (DADGAD; a Dsus4 tuning) for a while now and wanted to dig deeper into chords and scales in it. While there are lots of resources available for standard tuning, I’ve found few when it comes to alternate tunings like DADGAD. Thus my attempt to encode this information programmatically. Another reason is…well…fun!
Before starting, I just wanted to add a quick note on my previous article. My goal was explicitly to provide an algorithmic understanding of traditional Western music theory. Personally, I found it clearer to first understand music theory algorithmically before memorizing and practicing it (which one has to do to actually apply it in practice). Your mileage might vary of course. For those interested in learning more music theory, I can’t recommend Michael New’s playlist highly enough.
This article is fairly long, so here’s a brief outline: there are three main sections looking at programmatically (i) generating fretboard information, (ii) deriving chords, and (iii) deriving scales.
- Fretboard Information: In this section, we start with some background on the guitar fretboard. We then programmatically (i) encode key information, (ii) label notes, (iii) label intervals and (iv) derive pitch information for each fret.
- Chords: In this section we start exploring basic chords. We programmatically encode searching for simple three-note chords (triads) by first finding notes on a given string, then using that to find triad notes across multiple strings. We then implement a simple recursive algorithm to generate all possible chords. Finally we perform some playability optimization and explore triad inversions.
- Scales: In this section, we start deriving scales. Due to the 2D nature of the guitar fretboard, and the possibility of arbitrary tunings, we first implement some basic helpers: iterators for searching forward and backward from a given fret, calculating string wraparounds, and calculating frontiers or equivalents of a given note on other strings. Using these, we then look at a recursive algorithm for finding scales across the neck and for a way to filter them within a box of frets. Finally, I very briefly touch on optimizing scales for playability.
Fretboard Information
The guitar is a beast. It might look innocent enough, but due to the two-dimensional nature of the guitar fretboard, there’s a tendency for things to get really hairy. In this first section, we’ll dissect the fretboard a bit and encode our knowledge of it into a Python class.
The Guitar Fretboard
For the uninitiated, this is what a guitar fretboard looks like.

The image shows the notes on a 21-fret fretboard of a six string guitar tuned to standard tuning. That is, there are six strings (the horizontal lines) tuned to the notes E, A, D, G, B, and E from bottom to top (or from the thickest to thinnest strings). The pitch also increases from bottom to top; therefore the E at the top left (the orange circle) turns out to be two octaves higher than the E at the bottom left (the blueish-green circle).
Each fret (the vertical lines) is where the string makes contact when you press down on it (at the spot where the circles are in the above image). This shortens the length of the string and raises the frequency of the note. Frets are carefully spaced out on the guitar such that each successive fret is a half-note increment from the previous one. You can see this in the note labels on each fret in the image above (using only sharps, for simplicity). You’ll also notice that although there are 21 frets, you can have 22 notes per string if you include the open string (i.e. fret zero, or playing the open string with nothing pressed down).
Finally, we can note some basic relationships of notes on the fretboard: for every string, frets zero (the left-most circles) and twelve (the right-most orange circles) are identical notes but an octave apart. This is always true due to the design of the guitar where the twelfth fret sits exactly at exactly halfway between the nut and the bridge.
Second, and this is where things get whacky with the guitar, each note in the middle is identical to the same color note on fret zero of the next successive string. So for example, the two blue A’s are identical both in notation and pitch. There are five such notes for the six strings.
In fact, the diagram below shows how many ways the same B can be played on a 21-fret guitar. These are not B’s one octave after another, but rather identical in pitch.

While the twelve frets rule is inherent to the design of the guitar, the relationship of on which fret each string wraps around, so to speak, to the next successive one, depends entirely on the specific tuning being used. Alternate tunings, where some strings have a higher or lower pitch, will have these relationship similarly altered. You can see this below in a diagram similar to the previous one, but for DADGAD tuning:

Let’s now encode some of this knowledge programmatically in Python. We start by labeling notes and intervals based on a user-specified key. We then label notes with extra pitch information to detect octaves or equivalent notes like the B’s above.
Let’s start with a simple Fretboard class that generalizes over the number of strings, number of frets, the key we want to use, and the tuning:
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E']):
self.nstrings = nstrings
self.nfrets = nfrets
self.tuning = tuning
self.key = key
Note for consistency: I assume for the rest of this article that nfrets is the number of frets including fret zero. So a 21-fret guitar would have nfrets=22.
Key Information
If you’ve read my previous article, I showed how we can pick out notes from enharmonic equivalents based on a given key. We do this by using intervals, relative relationships between notes, to represent the notes we want in a key-agnostic way. So we already know how to map from intervals to notes in a key. Let’s also build a reverse map for this so we can map from notes to intervals.
from music_theory import make_intervals_major
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E']):
...
self.note_to_interval, self.interval_to_note = self.init_key_mappings(key)
self.notes_in_key = list(self.interval_to_note.values())
def init_key_mappings(self, key):
# Generate using code from previous article
interval_to_note = make_intervals_major(key)
# Now reverse the returned dict
note_to_interval = defaultdict(lambda: [])
for (interval, note) in interval_to_note.items():
note_to_interval[note].append(interval)
# Return both mappings
return dict(note_to_interval), interval_to_note
Above, we use the make_intervals_major() function from my previous post to generate mappings from intervals (relative to the major scale) to notes in a key. Using this data, the function further generates a reverse mapping. For each note, it calculates what interval it can be.
Here is what self.interval_to_note looks like for the key of C.
>>> from pprint import pprint
>>> f = Fretboard(nstrings=6, nfrets=21, key='C')
>>> pprint(f.interval_to_note)
{'#1': 'C#',
'#11': 'F#',
'#2': 'D#',
'#3': 'E#',
'#4': 'F#',
'#5': 'G#',
'#6': 'A#',
'#7': 'B#',
'1': 'C',
'11': 'F',
'13': 'A',
'2': 'D',
'3': 'E',
'4': 'F',
'5': 'G',
'6': 'A',
'7': 'B',
'8': 'C',
'9': 'D',
'b2': 'Db',
'b3': 'Eb',
'b4': 'Fb',
'b5': 'Gb',
'b6': 'Ab',
'b7': 'Bb',
'b8': 'Cb',
'bb2': 'Dbb',
'bb3': 'Ebb',
'bb6': 'Abb',
'bb7': 'Bbb'}
You can see that multiple interval names can have the same note (e.g. the trivial 1 and 8 are just the same note one octave apart). This is why the reverse mapping has an array for each note. Here is the reverse mapping for the key of C showing how notes map to intervals:
>>> from pprint import pprint
>>> f = Fretboard(nstrings=6, nfrets=21, key='C')
>>> pprint(f.note_to_interval)
{'A': ['6', '13'],
'A#': ['#6'],
'Ab': ['b6'],
'Abb': ['bb6'],
'B': ['7'],
'B#': ['#7'],
'Bb': ['b7'],
'Bbb': ['bb7'],
'C': ['1', '8'],
'C#': ['#1'],
'Cb': ['b8'],
'D': ['2', '9'],
'D#': ['#2'],
'Db': ['b2'],
'Dbb': ['bb2'],
'E': ['3'],
'E#': ['#3'],
'Eb': ['b3'],
'Ebb': ['bb3'],
'F': ['4', '11'],
'F#': ['#4', '#11'],
'Fb': ['b4'],
'G': ['5'],
'G#': ['#5'],
'Gb': ['b5']}
Finally, we also store a list of all notes that are relevant to us in the specified key using: list(self.interval_to_note.values()).
Labeling Notes
Now that we have key information in place, let’s start with encoding the actual fretboard itself.
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E']):
...
self.notes = [chromatic_wrapping(tuning[i], nfrets) for i in range(nstrings)]
Generating the notes on the fretboard is surprisingly easy. Remember the chromatic scale that consists of all the notes, each spaced apart by a half-note? Each string is just a looping chromatic scale starting with the note the string is tuned to.
The chromatic_wrapping() function above takes as argument the starting note (which here would be the tuning of a particular string), and the number of values to generate. We call chromatic_wrapping() for each string via a Python list comprehension (giving us a 2D list). Here is the code for the chromatic_wrapping() function:
from music_theory import chromatic
def chromatic_wrapping(key, n):
notes = chromatic(key)
return [notes[i % len(notes)] for i in range(n + 1)]
Above we generate a chromatic scale using the chromatic() function from my previous article. We then generate a list of size n, making sure to wrap around the notes variable using the modulo operator.
This will return all enharmonic equivalents when generating a string. Here is the output of a single call of chromatic_wrapping():
>>> from pprint import pprint
>>> pprint(chromatic_wrapping('C', 21))
[['B#', 'C', 'Dbb'],
['B##', 'C#', 'Db'],
['C##', 'D', 'Ebb'],
['D#', 'Eb', 'Fbb'],
['D##', 'E', 'Fb'],
['E#', 'F', 'Gbb'],
['E##', 'F#', 'Gb'],
['F##', 'G', 'Abb'],
['G#', 'Ab'],
['G##', 'A', 'Bbb'],
['A#', 'Bb', 'Cbb'],
['A##', 'B', 'Cb'],
['B#', 'C', 'Dbb'],
['B##', 'C#', 'Db'],
['C##', 'D', 'Ebb'],
['D#', 'Eb', 'Fbb'],
['D##', 'E', 'Fb'],
['E#', 'F', 'Gbb'],
['E##', 'F#', 'Gb'],
['F##', 'G', 'Abb'],
['G#', 'Ab']]
Each note above is represented by all the enharmonic equivalents possible. However, since we’re really only interested in notes of the specified key, we can filter these out with a simple function as shown below:
from pprint import pprint
def filter_by_key(scale, filter_list):
filtered = []
for notes in scale:
filtered.append([x for x in notes if x in filter_list])
return filtered
f = Fretboard(6, 21, 'C')
pprint(filter_by_key(chromatic_wrapping('C', 21), f.notes_in_key))
The notes_in_key information we derived in the previous section already pays off.
We get the following filtered notes; only the ones relevant to the key of C.
[['B#', 'C', 'Dbb'],
['C#', 'Db'],
['D', 'Ebb'],
['D#', 'Eb'],
['E', 'Fb'],
['E#', 'F'],
['F#', 'Gb'],
['G', 'Abb'],
['G#', 'Ab'],
['A', 'Bbb'],
['A#', 'Bb'],
['B', 'Cb'],
['B#', 'C', 'Dbb'],
['C#', 'Db'],
['D', 'Ebb'],
['D#', 'Eb'],
['E', 'Fb'],
['E#', 'F'],
['F#', 'Gb'],
['G', 'Abb'],
['G#', 'Ab']]
So coming back to our __init__() function, what we end up with is the following:
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E']):
...
self.notes = [chromatic_wrapping(tuning[i], nfrets) for i in
self.notes_filtered = [filter_by_key(
chromatic_wrapping(tuning[i], nfrets + 1),
self.notes_in_key
)
for i in range(nstrings)]
Ok, great! We now have the ability to encode the notes of a fretboard in a user-specified key. We can retrieve the note for any fret by looking up the string (from 0 to nstrings - 1) and fret (from 0 to nfrets):
>>> pprint(f.notes[0][0])
['E', 'Fb']
>>> pprint(f.notes[5][0])
['E', 'Fb']
>>> pprint(f.notes[0][12])
['E', 'Fb']
>>> pprint(f.notes[5][12])
['E', 'Fb']
We can do this trivially for arbitrary tunings as well. Here is an example for a D modal tuning where strings are tuned to DADGAD (instead of the EADGBE of standard tuning):
>>> f = Fretboard(6, 12, 'C', tuning=['D', 'A', 'D', 'G', 'A', 'D'])
>>> f.notes[0][0]
['D', 'Ebb']
>>> f.notes[5][0]
['D', 'Ebb']
>>> f.notes[0][12]
['D', 'Ebb']
>>> f.notes[5][12]
['D', 'Ebb']
Labeling Intervals
Similar to how we labeled notes for each fret, let’s label each fret with intervals as well. This is easy now that we generated our notes. We can look up the notes for a given fret, then use our note_to_interval dictionary and get the intervals associated with it.
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E']):
...
self.intervals = self.init_intervals()
def init_intervals(self):
# A 2D grid of empty lists
intervals = [[[] for fret in range(self.nfrets)] for string in range(self.nstrings)]
# For each string and fret
for string in range(self.nstrings):
for fret in range(self.nfrets):
# Iterate through the key-specific notes using self.notes_filtered
for note in self.notes_filtered[string][fret]:
# Map each note back to a list of intervals and append
intervals[string][fret] += self.note_to_interval[note]
return intervals
We can now also retrieve the intervals for any given fret:
>>> pprint(f.intervals[0][0])
['3', 'b4']
>>> pprint(f.intervals[5][0])
['3', 'b4']
>>> pprint(f.intervals[0][12])
['3', 'b4']
>>> pprint(f.intervals[5][12])
['3', 'b4']
The notes above correspond to an E in standard tuning, which in the key of C, does indeed correspond to a (major) third (a 3 interval) or a flattened fourth (a b4 interval).
Labeling Frets with Pitch Information
The final piece of information we’re going to generate is pitch information. Remember that each note can be in different octaves and we want to be able to derive this information for the guitar. Of course, this is a common problem, so there’s already a system in place for this: Scientific Pitch Notation (SPN).
In SPN, each musical note name is combined with a number to uniquely identify the pitch and the octave it sits in. The system begins at C0 and at every successive C note, the octave number goes up. So for example a C3 is a C note in the third octave, and is one octave lower than a C4. If you look at an instrument like the piano, it’s quite easy to visualize.

The guitar typically sits in the colored range of the keyboard above. A guitar in standard tuning has the layout shown below. The colored notes match the colors of the keyboard.

As you can see, the same note, with the same pitch can exist on multiple strings on the guitar.
The rules are fairly easy to encode though. Basically, when we see a C note, we increase the octave by one. And while traversing a string from left to right, when we observe a note that is the same as that on the zero’th fret of the next string, we record its octave number. We then process the next string starting with that saved value.
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E'], lowest_pitch=2):
...
self.pitches = self.init_pitches(lowest_pitch)
def init_pitches(self, lowest_pitch):
pitches = [[None for i in range(self.nfrets)] for j in range(self.nstrings)]
next_pitch = None
for string in range(self.nstrings):
next_pitch_set = False
current_pitch = lowest_pitch if string == 0 else next_pitch
for fret in range(self.nfrets):
if 'C' in self.notes[string][fret]:
current_pitch += 1
if (not next_pitch_set) and string < 5 and self.notes[string + 1][0] == self.notes[string][fret]:
next_pitch_set = True
next_pitch = current_pitch
pitches[string][fret] = current_pitch
return pitches
The first thing we do above is add a new parameter to the __init__ of our Fretboard class: lowest_pitch. It specifies the pitch of the lowest note on the lowest string and defaults to 2. We then process the rest of the strings using that.
The init_pitches() function is a fairly straightforward encoding of the rules described above. It does two things: (i) everytime it encounters a C note, it increments current_pitch by one, and (ii) everytime it encounters a note that is identical to that of the zero’th fret of the next string, it saves it in next_pitch (used for setting current_pitch when starting out processing the next string).
The only thing to note here is that we use self.notes, not self.notes_filtered for detecting a C note. Recall that self.notes_filtered contains the notes filtered to the specified key, while self.notes contains all notes. This is needed as one may specify a key that doesn’t have a C in it; using self.notes ensures we detect a pitch shift regardless of key.
What we end up with is a 2D array showing the pitches of each note. Here is the output we get if we pretty-print the pitches variable after init_pitches() has been called:
>>> f = Fretboard(6, 21, 'C')
>>> pprint(f.pitches)
[[2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4],
[2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4],
[3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5],
[3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5],
[4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6]]
Remember that the above output is a vertical flip of the image shown earlier: string 0 corresponds to the first line of output above, but represents the lowest string in the diagram (i.e. the bottom-most E string). We can output a diagram-style view of pitches by reversing the list before printing it out:
>>> f = Fretboard(6, 21, 'C')
>>> pprint(list(reversed(f.pitches)))
[[4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6],
[3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5],
[3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5],
[3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4],
[2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4]]
That brings us to the end of this first section where we encoded our fretboard knowledge into our Fretboard class. We’ll derive some more information later in the article, but for now let’s quickly recap: (i) we derived mappings between notes and intervals in a user-specified key, (ii) we derived a grid of notes and intervals for each fret on the fretboard, and (iii) we derived pitch information for every fret that lets us detect what octave the note on a fret sits in.
Let’s now have some fun: let’s try to find chords on the guitar neck with all the knowledge we’ve encoded.
Chords (Triads)
Chords are a complex topic. In particular, full chords that use all six strings can get complex to search for. However, we can start with the most basic chords: triads.
Triads consist of a stack of three notes that are each a third interval apart. This third interval can be either a major 3rd (3) or a minor 3rd (b3). This stacking of notes that are a third interval apart is the basic approach to building chords.
For example, four-note chords like the dominant 7th chords stack an additional third above the fifth (i.e. the seventh). More complex chords stack 9th, 11th, and 13th notes on top.
Major Triads on Sets of Three Strings
Let’s start with the simplest three-note chords: major triads. The major triad consists of the 1, 3 and 5 notes in a key played together. For the key of C these would be the notes C, E, and G, respectively. Since we have three notes, we can derive triads in any key for groupings of three strings at a time: [0, 1, 2], [1, 2, 3], [2, 3, 4], and [3, 4, 5].
For simplicity, let’s use a dict to specify this mapping of intervals and strings:
major_triad_on_strings_012 = {0: '1', 1: '3', 2: '5'}
major_triad_on_strings_123 = {1: '1', 2: '3', 3: '5'}
major_triad_on_strings_234 = {2: '1', 3: '3', 4: '5'}
major_triad_on_strings_345 = {3: '1', 4: '3', 5: '5'}
In the above examples, we use the string number as the key and the interval name as the value. In the next two sections we will first find a particular interval on a given string, and once we can do that, use a recursive algorithm to derive all possible chord shapes using the chord “specification” show above.
Finding a Given Interval on a String
Find a particular interval on a string is pretty trivial since we already have a mapping of frets to intervals (the intervals property of the Fretboard class). Note that what we get back is a list since a particular note may be at multiple locations on any given string. For example, a C note can be found on frets 8 and 20.
class Fretboard
...
def find_interval_on_string(self, interval, string):
return [index
for (index, fret_intervals)
in enumerate(self.intervals[string])
if interval in fret_intervals]
Above, I use a simple list comprehension to find the interval on the given string. I go through self.intervals[string] using enumerate() to give me an index (i.e. fret number). I then add a conditional check to ensure that the interval we want is on that fret.
Here is the output for find a 1 interval in the key of C (i.e. a C note) on all strings:
>>> f = Fretboard(6, 21, 'C')
>>> for string in range(6):
... print('{}:'.format(string), f.find_interval_on_string('1', string))
...
0: [8, 20]
1: [3, 15]
2: [10]
3: [5, 17]
4: [1, 13]
5: [8, 20]
Those are the correct frets on the guitar where you find the C note (in standard tuning)!
Finding Triads
Given a triad formula, which map strings to intervals, we can now derive the locations of each note on the requested strings:
class Fretboard:
...
def find_all_notes2(self, mapping):
return {string: self.find_interval_on_string(interval, string)
for string, interval in mapping.items()}
Given a mapping of strings to intervals (e.g., {0: '1', 1: '3', 2: '5'}), the above function uses a Python dict comprehension to generate a mapping of strings to frets on that string.
Here is an example of the output we get:
>>> f = Fretboard(6, 21, 'C')
>>> pprint(f.find_all_notes({0: '1', 1: '3', 2: '5'}))
{0: [8, 20], 1: [7, 19], 2: [5, 17]}
While that’s nice, we want to know which frets to press; not just where we can find these notes on each string.
To do this, we calculate each permutation of the above possible locations and generate all possible chords. We can then run it through some basic optimization to filter out the “unplayable” versions.
Recursively Generate All Possible Chords
There are many ways to generate all the possible permutations of finger positions, but I’ve chosen a simple recursive algorithm here. This is find as the depth of recursion is limited to a maximum of six since that’s the number of strings we have.
class Fretboard:
...
def find_all_chords(self, search_space, current_finger_pos, solutions, level=0):
remaining = [x for x in current_finger_pos if current_finger_pos[x] == None]
if remaining == []:
solutions.append(current_finger_pos)
return None
pick = remaining[0]
for potential in search_space[pick]:
new_finger_pos = current_finger_pos.copy()
new_finger_pos[pick] = potential
self.find_all_chords(search_space, new_finger_pos, solutions, level+1)
if level == 0:
return solutions
The above recursive algorithm is fairly simple and just bruteforces every possible finger position for the given chord. It starts by first picking out all the strings that haven’t been assigned a fret number. From that we pick one string. We then loop through each possible position we could play on that string, set it, and recursively call the same function. The next iteration would search on the next unset string and so on until there are no more strings remaining to search. At that point the recursive calls return and all possible solutions are returned.
Here is an example of how to call this function:
>>> search_space = f.find_all_notes({0: '1', 1: '3', 2: '5'})
>>> pprint(search_space)
{0: [8, 20], 1: [7, 19], 2: [5, 17]}
>>> initial_finger_pos = {x: None for x in search_space}
>>> pprint(f.find_all_chords(search_space, initial_finger_pos, []))
[{0: 8, 1: 7, 2: 5},
{0: 8, 1: 7, 2: 17},
{0: 8, 1: 19, 2: 5},
{0: 8, 1: 19, 2: 17},
{0: 20, 1: 7, 2: 5},
{0: 20, 1: 7, 2: 17},
{0: 20, 1: 19, 2: 5},
{0: 20, 1: 19, 2: 17}]
Initially, for every string we set the value in initial_finger_pos to None. The solutions generated are basically every possible permutation of search_space.
Basic Playability Optimization
Now of course some of these combinations are crazy. For example, to play {0: 20, 1: 19, 2: 5}, you need to stretch your fingers across 16 frets.
So let’s write a simple function to find the version with the lowest “finger span”:
>> positions = f.find_all_chords(search_space, {x: None for x in search_space}, [])
>> pprint(filter_min_span(positions))
[{0: 8, 1: 7, 2: 5}, {0: 20, 1: 19, 2: 17}]
That’s more like it! These two solutions are identical, and just spaced 12 frets, or one octave, apart. Here is what this looks like on the fretboard:

Since these are just an octave apart, we might as well write a function to pick out the lowest one:
def filter_lower(solutions):
pos = [min(x.values()) for x in solutions]
return [x for i, x in enumerate(solutions) if pos[i] == min(pos)]
Example: Generating All Major Triads in a Key
Let’s now try to generate all possible C major triads across groups of three strings:
for a, b, c in [(0, 1, 2), (1, 2, 3), (2, 3, 4), (3, 4, 5)]:
search_space = f.find_all_notes({a: '1', b: '3', c: '5'})
positions = f.find_all_chords(search_space, {x: None for x in search_space}, [])
pprint(filter_lower(filter_min_span(positions)))
And here is the output we get:
[{0: 8, 1: 7, 2: 5}]
[{1: 3, 2: 2, 3: 0}]
[{2: 10, 3: 9, 4: 8}]
[{3: 5, 4: 5, 5: 3}]
This corresponds to the following positions:
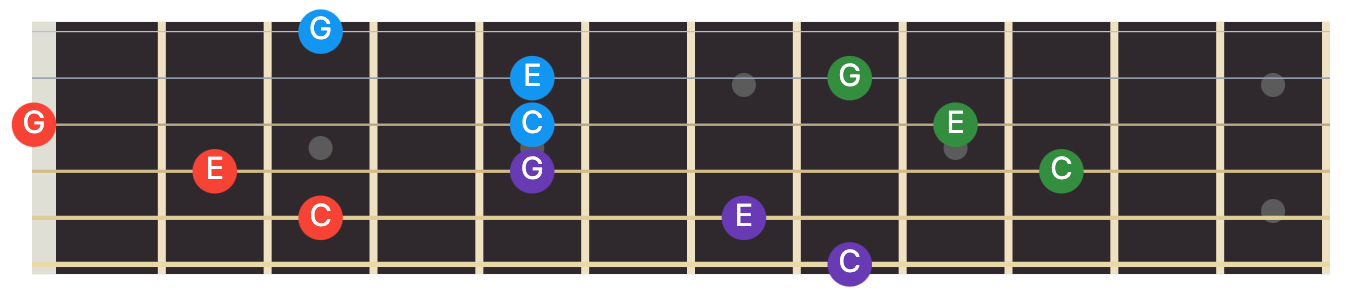
More Triads
We can of course also go beyond just major triads and generate any of the triads from our set of formulas:
chords = {
# Major
'major': '1,3,5',
'major_6': '1,3,5,6',
'major_6_9': '1,3,5,6,9',
'major_7': '1,3,5,7',
'major_9': '1,3,5,7,9',
'major_13': '1,3,5,7,9,11,13',
'major_7_#11': '1,3,5,7,#11',
# Minor
'minor': '1,b3,5',
'minor_6': '1,b3,5,6',
'minor_6_9': '1,b3,5,6,9',
'minor_7': '1,b3,5,b7',
'minor_9': '1,b3,5,b7,9',
'minor_11': '1,b3,5,b7,9,11',
'minor_7_b5': '1,b3,b5,b7',
# Dominant
'dominant_7': '1,3,5,b7',
'dominant_9': '1,3,5,b7,9',
'dominant_11': '1,3,5,b7,9,11',
'dominant_13': '1,3,5,b7,9,11,13',
'dominant_7_#11': '1,3,5,b7,#11',
# Diminished
'diminished': '1,b3,b5',
'diminished_7': '1,b3,b5,bb7',
'diminished_7_half': '1,b3,b5,b7',
# Augmented
'augmented': '1,3,#5',
# Suspended
'sus2': '1,2,5',
'sus4': '1,4,5',
'7sus2': '1,2,5,b7',
'7sus4': '1,4,5,b7',
}
def make_chord_mapping(strings, name):
intervals = chords[name].split(',')
return {x: intervals[i] for i, x in enumerate(strings)}
This lets us make any mapping quickly given a set of strings and a formula name:
>>> print(make_chord_mapping((0, 1, 2), 'major'))
{0: '1', 1: '3', 2: '5'}
Triad Inversions
Triad inversions are just left rotations of the triad formula. For example, in what’s called the default root position of the major triad [1, 3, 5], the 1 is the lowest note played. In the first inversion, you rotate left to get [3, 5, 1], with the major third being the lowest note. And the third and final possibility is the second inversion where the fifth becomes the lowest note: [5, 1, 3]. For four-note chords, we can also have a 3rd inversion.
We can generate these from our above formulas easily:
def inversion(formula, n):
return formula[n:] + formula[:n]
def first_inversion(formula):
return inversion(formula, 1)
def second_inversion(formula):
return inversion(formula, 2)
def third_inversion(formula):
return inversion(formula, 3)
>>> print(first_inversion('major'))
3,5,1
>>> print(second_inversion('major'))
5,1,3
>>> print(third_inversion('major_7'))
7,1,3,5
Finding Full Chords?
The chords we’ve derived are small chord fragments that are the basis of chords that use four, five, or six strings. The basic idea is to extend copies of the same notes to the other strings. I haven’t looked too deeply into this just yet so instead I’ll just jot down some thoughts if you want to try and tackle this yourself:
- You need to maintain the lowest note based on the inversion of the triad you’re trying to expand into a full chord. Adding a lower note that is a third or fifth would change the flavor of a root triad.
- Strings might need to be muted. Muted strings are when you block the sound of certain strings because you can’t find an easy way to play the notes of the chord within it. These need to be playable.
- With string muting, you also need to make sure essential notes are not removed from the chord. For example, removing the fifth entirely would make the chord lose its flavor.
- Chords may need to be moveable, or may work with open strings in the given tuning.
I’m going to leave chords here for now. Lets quickly recap: (i) we first wrote a function to find a particular interval on a string, (ii) found possible positions for finger positions given a mapping from strings to intervals, (iii) implemented a recursive algorithm for generating all permutations, and (iv) performed some basic optimization for playability. Finally, we looked at other chord formulas, and how to generate chord inversions.
Let’s now move on to a far more complex topic: scales.
Scales
Scales are sets of notes ordered by pitch. An example is the major scale we looked at in my previous article. In this section, we will look at deriving ascending scales, that is scales ordered by increasing pitch, on the guitar fretboard.
The approach I took is fairly basic: start at a root note somewhere on the fretboard, and proceed to increase pitch based on the scale pattern we want.
The problem is that, as we saw before, the same note with identical pitch may be found on multiple strings at different frets. The question then becomes: given a note on the fretboard somewhere, and asked to find the next successive note after it (e.g. given a 1 note, find the 2 note that follows it), how do we search for it? A similar question can be asked when descending scales (although we will not look at this in too much detail in this article).
Find Interval Forward and Backward
Let’s look at finding an interval going forward from a given note. Suppose we are given an E note on the second-highest string, as shown in the image below, and asked to find the F that comes after it in pitch.

A first attempt might be to start at the starting note, traverse till the end of the string and, continue on the next string until we find a valid F note.
That doesn’t actually work though. This is where the 2D structure of the guitar fretboard bites us. Remember, that the E note in the above image actually has equivalents across the other strings. In fact, on the 24-fret diagram shown below, you can see that every single string has an equivalent E note of the same pitch.
Taken together, we can see that these notes form a sort of frontier for our given note. If asked to find notes higher in pitch, we should search on each string on all frets that sit to the right of this frontier (as shown by the green arrows in the diagram below). Similarly, for find a note that has a lower pitch, that is searching backwards, we can imagine a frontier that sits on fret behind each E; we would need to search all frets on all strings to the left of this “backward frontier”.

The good news is that this frontier pattern is identical for any given note and only depends on the tuning we’re in. Therefore, we can just derive this frontier in our __init__() function. Second, the way to derive this frontier is just to observe when strings wrap around!
Remember how earlier in this article we set the pitch of the zero’th fret on the next string when we observed the same note on the current string? What we want is just a generalized version of that: given a note on a string at some fret, where will it be on all other strings?
Calculating String Wraparounds
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E'], lowest_pitch=2):
...
self.wraparounds = self.init_wraparounds()
def init_wraparounds(self):
wraparounds = [0 for x in range(self.nstrings)]
for string in range(self.nstrings):
for fret in range(self.nfrets):
if (string < 5 and
self.notes[string + 1][0] == self.notes[string][fret] and
self.pitches[string + 1][0] == self.pitches[string][fret]):
wraparounds[string] = fret
return wraparounds
The above function tells us at what fret one string has an equivalent on fret zero of the next string. Here is an example for standard tuning:
>>> f = Fretboard(6, 21)
>>> print(f.wraparounds)
[5, 5, 5, 4, 5, 0]
The output can be interpreted as:
- The 5th fret of string 0 is equivalent to fret 0 of the string 1.
- The 5th fret of string 1 is equivalent to fret 0 of the string 2.
- The 5th fret of string 2 is equivalent to fret 0 of the string 3.
- The 4th fret of string 3 is equivalent to fret 0 of the string 4.
- The 5th fret of string 4 is equivalent to fret 0 of the string 5.
- String 5 has no next string it wraps around on (since we only strings 0 through 5).
Calculating Frontiers
Given a note (via a string and fret), we want to know the frets on the other strings where it has equivalents.
These offsets can be calculated easily using the wraparound information.
class Fretboard:
def __init__(self, nstrings, nfrets, key, tuning=['E', 'A', 'D', 'G', 'B', 'E'], lowest_pitch=2):
...
self.offsets = self.init_per_string_offsets()
def init_per_string_offsets(self):
'''Find the offsets of equivalent frets relative to each string'''
offsets = []
offsets0 = [-sum(self.wraparounds[:string]) for string in range(self.nstrings)]
for string in range(self.nstrings):
offsets.append([x - offsets0[string] for x in offsets0])
return offsets
Terrible attempt at an explanation: The above function takes a cumulative sum of self.wraparounds for each string (starting with string zero and up to the string in question) to get the offsets for string 0. It then uses that to calculate the offsets for each string.
If that made no sense, that’s fine. The code above is a little confusing so lets focus on the output instead:
>>> f = Fretboard(6, 21)
>>> pprint(f.offsets)
[[0, -5, -10, -15, -19, -24],
[5, 0, -5, -10, -14, -19],
[10, 5, 0, -5, -9, -14],
[15, 10, 5, 0, -4, -9],
[19, 14, 9, 4, 0, -5],
[24, 19, 14, 9, 5, 0]]
The way to interpret this is as follows: there are six lists inside f.offsets, one for each string. Each one represents the offsets that must be added to a note on that string in order to derive the equivalent note on other strings.
So for example, our E note below is on string 4 (starting at index 0 from the bottom), and fret 5.

Since we’re dealing with string 4, we take the values for it from f.offsets[4]. We get the list [19, 14, 9, 4, 0, -5]. If we take the fret number of our E (5) and add it to each of these offsets, we get [24, 19, 14, 9, 5, 0]. These are the frets on which this note has equivalents on each string. This corresponds with our original image of equivalents as can be seen below:

We can encode the above calculation as a simple frontier() function that finds the frontier for any given note (specified as a string number and fret number):
class Fretboard:
...
def frontier(self, string, fret):
'''Given a fret, find its equivalents on all strings'''
return [x + fret for x in self.offsets[string]]
Iterating Forward From a Note
To iterate forward from a given note (specified as a string and fret), we write a simple generator as shown below:
class Fretboard:
...
def iter_forward(self, start_string=0, start_fret=0, strict=False):
frontier = self.frontier(start_string, start_fret)
for string in range(self.nstrings):
for fret in range(max(frontier[string] + (1 if strict else 0), 0), self.nfrets):
yield (string, fret, self.intervals[string][fret])
Given a start_string and start_fret, the iter_forward() function first finds the frontier of that note. It then iterates from the frontier position on each string until the end of the string, each time calling yield. For each yield, it provides a tuple with the string number, fret number, and the intervals associated with that location. The strict parameter can be used to specify whether to search strictly above the specified fret (exclusive of it) or inclusively.
The output for our E note on string 4, fret 5 is shown below. You can verify it’s correctness using the image above if you like; all the frets searches should be to the right of the frontier formed by the E note.
>>> f = Fretboard(6, 21)
>>> pprint(list(f.iter_forward(4, 5)))
[(1, 19, ['3', 'b4']),
(1, 20, ['#3', '4', '11']),
(2, 14, ['3', 'b4']),
(2, 15, ['#3', '4', '11']),
(2, 16, ['#4', '#11', 'b5']),
(2, 17, ['5', 'bb6']),
(2, 18, ['#5', 'b6']),
(2, 19, ['6', '13', 'bb7']),
(2, 20, ['#6', 'b7']),
(3, 9, ['3', 'b4']),
(3, 10, ['#3', '4', '11']),
(3, 11, ['#4', '#11', 'b5']),
(3, 12, ['5', 'bb6']),
(3, 13, ['#5', 'b6']),
(3, 14, ['6', '13', 'bb7']),
(3, 15, ['#6', 'b7']),
(3, 16, ['7', 'b8']),
(3, 17, ['#7', '1', '8', 'bb2']),
(3, 18, ['#1', 'b2']),
(3, 19, ['2', '9', 'bb3']),
(3, 20, ['#2', 'b3']),
(4, 5, ['3', 'b4']),
(4, 6, ['#3', '4', '11']),
(4, 7, ['#4', '#11', 'b5']),
(4, 8, ['5', 'bb6']),
(4, 9, ['#5', 'b6']),
(4, 10, ['6', '13', 'bb7']),
(4, 11, ['#6', 'b7']),
(4, 12, ['7', 'b8']),
(4, 13, ['#7', '1', '8', 'bb2']),
(4, 14, ['#1', 'b2']),
(4, 15, ['2', '9', 'bb3']),
(4, 16, ['#2', 'b3']),
(4, 17, ['3', 'b4']),
(4, 18, ['#3', '4', '11']),
(4, 19, ['#4', '#11', 'b5']),
(4, 20, ['5', 'bb6']),
(5, 0, ['3', 'b4']),
(5, 1, ['#3', '4', '11']),
(5, 2, ['#4', '#11', 'b5']),
(5, 3, ['5', 'bb6']),
(5, 4, ['#5', 'b6']),
(5, 5, ['6', '13', 'bb7']),
(5, 6, ['#6', 'b7']),
(5, 7, ['7', 'b8']),
(5, 8, ['#7', '1', '8', 'bb2']),
(5, 9, ['#1', 'b2']),
(5, 10, ['2', '9', 'bb3']),
(5, 11, ['#2', 'b3']),
(5, 12, ['3', 'b4']),
(5, 13, ['#3', '4', '11']),
(5, 14, ['#4', '#11', 'b5']),
(5, 15, ['5', 'bb6']),
(5, 16, ['#5', 'b6']),
(5, 17, ['6', '13', 'bb7']),
(5, 18, ['#6', 'b7']),
(5, 19, ['7', 'b8']),
(5, 20, ['#7', '1', '8', 'bb2'])]
Finding Scales Across the Neck
Finding a scale starting at a given string and fret can now be done fairly easily. You find notes and intervals in the scale sequence, but only using our find_interval_forward() function to progressively move forward in pitch. Since find_interval_forward() returns a list of equivalents of the interval being searched, we can write a simple recursive function as shown below. (Again, there are far more efficient ways to implement this, but the physical limit of the fretboard imposes a natural limit to the recursion depth.)
class Fretboard:
...
def solve_scale(self, intervals, start_string, start_fret, level=0):
out = []
if intervals == []:
return None
locations = self.find_interval_forward(intervals[0], start_string, start_fret)
for location in locations:
fragments = self.solve_scale(intervals[1:], location[0], location[1], level + 1)
out.append({'note': location, 'children': fragments})
return out
Above, solve_scale() finds all the locations where the first note of the remaining scale sequence exists, starting at the provided string and fret. For each location it finds, it calls solve_scale() for the remaining intervals of the scale.
Essentially, what we’re creating is a search tree that can be traversed to find all solutions:
def traverse(scales):
output = []
for x in scales:
if x['children'] is None:
output.append([x['note']])
else:
for fragment in traverse(x['children']):
output.append([x['note']] + fragment)
return output
>>> f = Fretboard(6, 21, 'C')
>>> scales = f.solve_scale(['1', '2', '3', '4', '5', '6', '7', '8'], 0, 0)
>>> pprint(scales)
[[(0, 8), (0, 10), (0, 12), (0, 13), (0, 15), (0, 17), (0, 19), (0, 20)],
[(0, 8), (0, 10), (0, 12), (0, 13), (0, 15), (0, 17), (0, 19), (1, 15)],
[(0, 8), (0, 10), (0, 12), (0, 13), (0, 15), (0, 17), (0, 19), (2, 10)],
...
[(1, 3), (2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (4, 0), (2, 10)],
[(1, 3), (2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (4, 0), (3, 5)],
[(1, 3), (2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (4, 0), (4, 1)]]
>>> print(len(scales))
21600
Whoa! That’s 21,600 unique ways to play a single octave of the C scale starting at the lowest string. Of course many of these combinations are not playable due to the physical limits of…well…our hands.
Let’s look at some basic ways to winnow this list down.
Finding Scales in a Box
A common approach to finding scales on the guitar is to find them within a “box” where you fingers can reach with a fixed anchor position. For example, scales in the first position would be those that can be played within the first four frets (assigned one finger each).
We can write a simple function that ensures all found notes lie within a certain minimum and maximum limit of both strings and frets:
def filter_boxed(solutions, min_string, min_fret, max_string, max_fret):
filtered = []
for solution in solutions:
strings = list(map(lambda x: x[0], solution))
frets = list(map(lambda x: x[1], solution))
if min(frets) < min_fret or max(frets) > max_fret:
continue
if min(strings) < min_string or max(strings) > max_string:
continue
filtered.append(solution)
return filtered
Now if we try to filter our list of 21,600 scales to limit it to, for example, the first three frets (for a total of four frets including fret zero) on all strings, we get exactly one solution:
>>> pprint(filter_boxed(patterns, 0, 0, 5, 3))
[[(1, 3), (2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (4, 0), (4, 1)]]
That’s actually a fairly standard way to play a C major scale in the first position!
Playability Optimization: An Initial Attempt
This article has already gotten pretty long, and attempting to derive scales with playability in mind (beyond just searching in boxes) is a longer topic. I won’t try to go into too much detail here, but rather just list some constraints that you might want to think about if you explore this further.
For playability, you want to assign fingers for each note in the scale and score it based on how easy it is to play (or discard it if it’s impossible to play). Finding this “cost” of a scale imposes a bunch of constraints, which you will have to figure out how to encode:
- Lower frets vs. higher frets. For novice players, lower frets are easier to press and are typically taught first.
- Avoiding hand position changes. You don’t want to be jumping around all over the fretboard while playing a scale.
- Four-finger placement. You want to try and make it so the four fingers align well with the scale notes. Typically the index finger plays one fret, the middle finger the fret after it, the ring finger the fret after that, and finally the little finger plays the fourth or fifth fret. This minimizes hand movement and makes playing a scale that adheres to this placement very efficient.
- Must avoid using the same finger for two consecutive notes.
- Fingers shouldn’t cross over each other.
- Finger strength: the index and middle fingers are generally stronger than the ring and little fingers.
- Preparing for successive notes: you want to find the next note such that the one after that will also be easy to play.
- Physical limits: there are limits on how much you can stretch your fingers or how quickly you can switch hand positions.
- Playing consecutive notes on different strings is hard and results in a choppy-sounding scale.
I have some initial code here on this gist, but it’s extremely rudimentary; just explorations. If you’re interested in looking deeper into this topic, maybe take a look. Since the problem is somewhat self-contained, it might also make sense to explore using an SMT solver like Z3 to optimize finger placement.
Conclusion
Phew! In this article we went through quite a bit of stuff. Let’s quickly recap.
We started by incorporating our knowledge of the fretboard in Python; this included key information, note and interval information, pitch information, note wraparounds on consecutive strings, and offsets for calculating equivalents. We used this to write code that helps derive triads (three-note chords) and apply some basic playability optimizations to the generated solutions. We also looked at generating chord inversions in code. Finally, we looked at the more complex problem of scales (notes played in sequence). We wrote code to help us search forward and backward from a given note, correctly accounting for equivalent notes on other strings. We then used that to find scales across the neck and apply some basic optimizations for playability.
Overall, this was a fun exercise in applying some of the basic theory I wrote about last time to an instrument that’s close to my heart. Hope you enjoyed!